Convolution at first seems like an intimidating and complex calculation. After examining the process step by step, it is easy to understand and perform.
The steps of convolution are: evaluate the two functions used as input (integrands). Next, evaluate the functions for all values in the range of the bounds. Finally, sum the evaluated points to calculate the output. Numerical integration techniques are used for quick and accurate calculation.
These steps can be accomplished using simple addition, multiplication, and integration. These steps are quickly performed by modern computers and result in several interesting properties.
What Are the Properties of Convolution?
Table of Contents
Convolution is a popular tool that has applications in many areas including signal processing and filtering, audio, image recognition, machine learning, and many more. With so many uses it is important to understand some of the common properties.
The properties of convolution are a set of common mathematical properties including commutativity, associativity, and distributivity. Convolution inherits these properties from multiplication and results from the fact that these properties also hold true for sums and integrals.
The Commutative Property is that the order of the inputs in the convolution does not affect the output. The Associative Property means that the grouping of the inputs does not affect the output of the convolution. Finally, the Distributive Property means that adding a new input to one of the existing inputs means performing the convolution with the added input too. [3]
Some common examples and special cases of convolution include:
- Auto-Regression Models
- Moving Average Models
- Auto-Correlation
- Cross-Correlation
- Low Pass Filters
- High Pass Filters
- Linear Filters
One common use of convolution for finance is to add together probability distributions. In the next section, I’ll cover this process!
How Do You Add Two Probability Distributions?
When examining random variables it is common to need to model how they interact. Frequently, the modeler needs to investigate the result of adding or subtracting random variables.
Two probability distributions are added by taking the density function of one and performing convolution with the other density function. The output of the convolution is the probability density of the two variables added together.
The primary method of calculating the probability density function (PDF) of two independent random variables involves using convolution. By taking the PDF of each input random variable and performing convolution, the resulting output is the PDF of the two random variables added together.
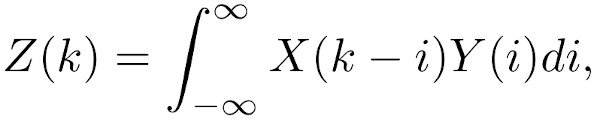
The random variable Z=X+Y where X and Y are two independent random variables. By calculating the convolution of the two density functions, the PDF of the added random variables is produced.
The PDFs of the random variables are evaluated over the entire range from negative infinity to positive infinity. The integration variable i represents each point in the PDF.
According to the Central Limit Theorem, by repeatedly taking the convolution of the PDFs of random variables, the output PDF will converge to a stable distribution. For fat-tailed probability distributions, the stable distribution is called the Levy-Stable distribution. For thin-tailed probability distributions, the stable distribution is the Normal distribution – which is also a special case of the Levy-Stable distribution. [4]
This covers the distribution and in the next section, I’ll cover simple formulas for adding the parameters of the distribution like mean and variance.
| alpha Value (Tail Thickness Parameter) | Converges to Distribution |
|---|---|
| 0 < a < 1.0 | Levy-Stable (Infinite Mean) |
| a = 1.0 | Cauchy |
| 1.0 < a < 2.0 | Levy-Stable (Infinite Variance) |
| a = 2.0 (all Thin-Tailed distributions) | Normal Distribution |
Adding Two Independent Variables
Adding two independent random variables leads to some helpful general formulas. First, regardless of whether the two variables are independent or dependent, it is generally true that the equation for the means is:
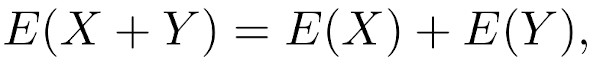
So adding the means (expected value) of two variables X and Y will have a mean which is the sum of the two input means. In contrast, the easy formula for the variance requires the variables X and Y to be independent:
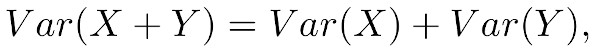
The situation changes some when repeatedly adding the same random variable in a repeated sum. This situation happens frequently when calculating the returns of financial data. Examples using python with historical data will be covered later in the post. By repeatedly summing the observed returns with mean mu, it propagates the observed returns forward in time.
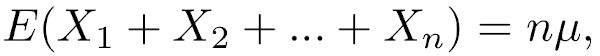
To calculate the mean of the returns on day n, the mean mu is simply multiplied by n. This simple formula requires that the random variables are independent and identically distributed. For calculating the variance of repeatedly summed random variables:
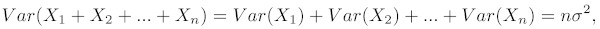
By summing the variances of the random variable, the variance of the result is simply n times the variance of the original random variable. This formula also requires the random variables to be independent and identically distributed. [4]
When calculated on computers, convolutions are implemented as discrete sums. In the next section, I’ll cover convolution sums.
What Are the Properties of a Convolution Sum?
Convolution sums are frequently used in applications like signal processing and filtering, as well as control systems and robotics. These sums have some common properties.
The properties of a convolution sum are the same as the properties of other sums. These include linearity, commutativity, associativity, closure, and additive identity. Calculating a convolution sum is a common way to mix two input signals.
The output of a Linear Time-Invariant System (LTI) can be calculated using a Convolution Sum. An example of such systems include motors, basic electrical circuits, and rudimentary control systems like a thermostat and a car’s cruise control. By using a convolution sum, the outputs for these systems can be calculated quickly and reliably by a computer or small microprocessor.
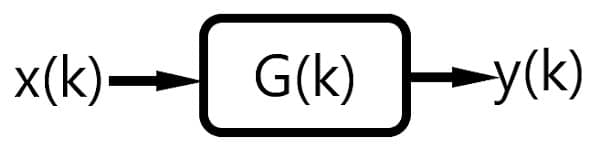
Represented as an equation, the convolution sum is as follows: [2]
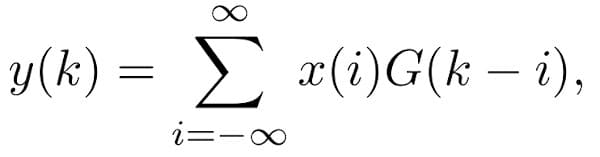
where each i is a time-shifted signal. The equation may look intimidating at first, but the explanation is fairly intuitive. For this convolution, the time invariance property is crucial. This property means that the response of the system (i.e. motor or circuit) does not change in time.
First, the input signal x can be represented as a sequence of single impulse inputs. An impulse input is a ‘jolt’ at a single point in time. For a motor, this might be giving a burst of power for a moment or instantaneously disturbing the load. The representation as a sequence of impulse inputs is possible because of the time invariance property. In the equation, this input sequence is represented by the x(i) where i is the input at each time step.
Exploring the unknown requires tolerating uncertainty
Brian Greene [6]
At each time step, the system’s response from all of the previous inputs is still present. For example, if a motor is momentarily powered it will continue to spin for a few moments afterward. This response is represented in the convolution sum by the G(k – i) term. The response is applied at current time step k and contains the responses from all other time steps i. By summing over all time steps, the convolution is calculated.
An alternative way of looking at the convolution is taking the time-shifted impulse response of the system and scaling it (multiplying) by the input. Other than the requirements of the LTI system, the properties of the convolution sum are the same as the properties of sums generally:
- Linearity
- Commutativity
- Associativity
- Closure
- Additive Identity
In practice, an infinite series is not often encountered if modeling something real like a motor. However, the properties of infinite series can also be used for convolution sums. These include convergence and divergence tests and replacing the infinite series with the value to which it converges. Since the system is LTI, the convolution sum can also be re-indexed to a different point in time.
The continuous version of the convolution sum is the convolution integral. Next, I’ll detail the continuous convolution.
What Are the Properties of a Convolution Integral?
Convolution integrals are used when evaluating continuous signals and mixing them together. There are several properties common to convolution integrals.
The properties of a convolution integral are the same as the properties of other integrals. These include the sum and difference rules, moving constants into and out of the integral, reversing the integration bounds negates the value, and the fundamental theorem can be used to evaluate it.
After covering the properties of convolution sums, the properties of convolution integrals are incredibly similar. The main difference is that a convolution integral is applied to continuous systems instead of discrete systems. This means that the time step in the system is infinitesimally small and becomes continuous. As a result, the convolution sum becomes a convolution integral.
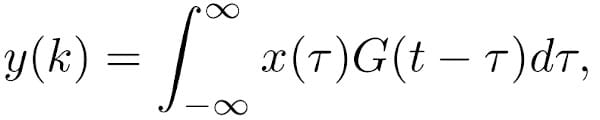
In this case, the t is the time point the convolution is evaluated, and the tau variable is the time step for evaluating the system response. Similar to the convolution sum formula, the x is the input signal and the G is the system response signal.
The properties of convolution integrals include the properties of normal integrals. These include: [3]
- The integral sum and difference rules.
- Being able to move multiplicative constants in and out of the integral.
- By reversing the integration bounds it multiplies the integral by a -1.
- Integrating bounds of zero length equals zero.
- Adding the intervals requires the integrand to be the same.
- The fundamental theorem of calculus is used to evaluate the integral.
The same interpretation of the convolution sums applies to the convolution integral. By taking the time-shifted impulse response of the system and scaling it (multiplying) by the input, the convolution is performed.
As is true for the convolution sum, the convolution integral also has the property of Commutativity and the property of Associativity. On computers, there is also a faster way to calculate convolutions by exploiting the Fast Fourier Transform (FFT).
What is FFT Convolution?
Directly evaluating convolution integrals can be a costly process computationally. If the function is complex and uses a large number of samples it can require a faster method.
FFT Convolution is using the Fast Fourier Transform (FFT) to evaluate convolutions using a faster method than directly calculating the integral. Using the transform the integration problem is converted into simple multiplication. After multiplying, the result is transformed back.
There is a theorem called the Convolution Theorem which provides a significant speed boost when calculating convolutions using a computer. The Convolution Theorem states that:
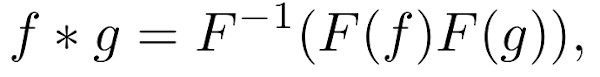
where * denotes convolution of signal functions f and g, and F denotes the Fourier Transform. Using this technique, the convolution integral is converted into ordinary multiplication. In addition, if convolution needs to be applied repeatedly the result can be multiplied in frequency space before applying the inverse transformation only once at the end. [1]
The advantage is that the costly FFT and FFT inverse operations need only be performed once at the beginning and end, and otherwise, the calculation is pure multiplication. In python’s scipy library, this is implemented using the fftconvolve function.
Some common library implementations provide additional speed tweaks under the hood. Often, padding the signal with zeros needs to be performed to prevent the output from shifting. In addition, it is common to pad the size to the closest power of two for a performance boost. For large signal sizes, the FFT convolution algorithm is O(n * log(n)) complexity. For small sizes n, it is faster to directly evaluate the convolution integral. [3]
Finally, let’s look at some visual examples of convolution using the Potion Analytics tools.
Convolution in Potion Analytics
The Potion Analytics tools are a set of python libraries for modeling and simulating the payoffs and probabilities for financial options. Primarily the analysis is focused on the Kelly Criterion. I helped make the Potion Analytics tools as part of the team with Ntropika Labs.
If you are interested in the project, check out the Ntropika Labs discord. The Potion DAO has its own discord for the Potion protocol as well.
Convolution is used in finance to look at probability distributions that are propagated forward in time from the current point. Suppose that one wanted to examine the probability a stock reaches a certain price one week from now. There are two ways one could do this.
Using a Historical Histogram
First, you could take the historical price data, calculate the return for each 1 week period and add it to a histogram. This histogram could be used to estimate the probabilities 1 week into the future. The drawback of this method is that it would only produce 52 samples in the histogram for every year of price data. This ratio gets worse and worse the further into the future the probability is examined. For one year into the future, there is one sample.
Using Convolution
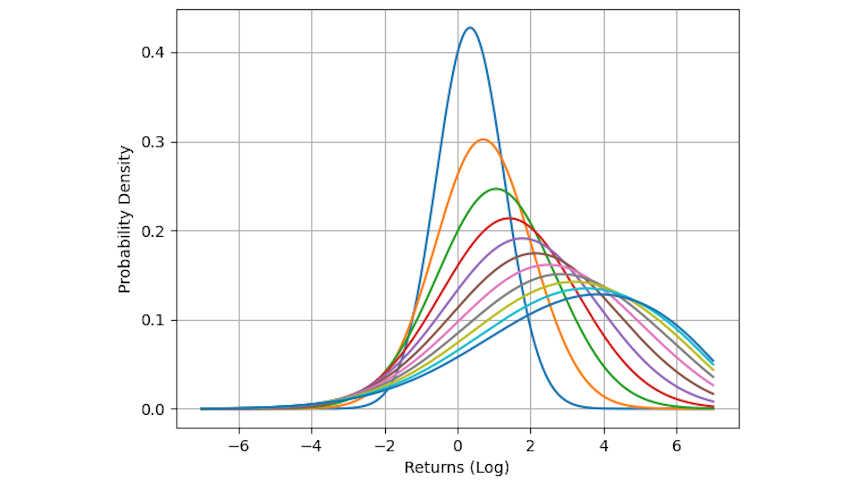
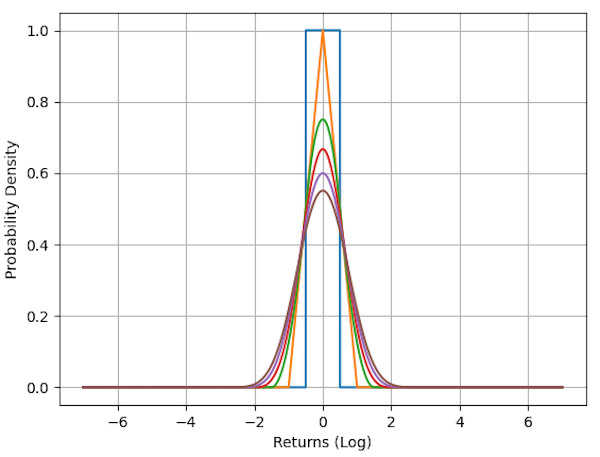
A better technique involves taking the 1-day histogram and using Convolution to propagate it forward in time. By taking the 1-day probability distribution and performing convolution with itself, the 2-day probability distribution is created (assuming the returns from one day to the next are independent).
This process can be repeated arbitrarily into the future to produce a probability distribution for any day. The main advantage is that this method does not suffer from having too few samples like the historical histogram method. [5]
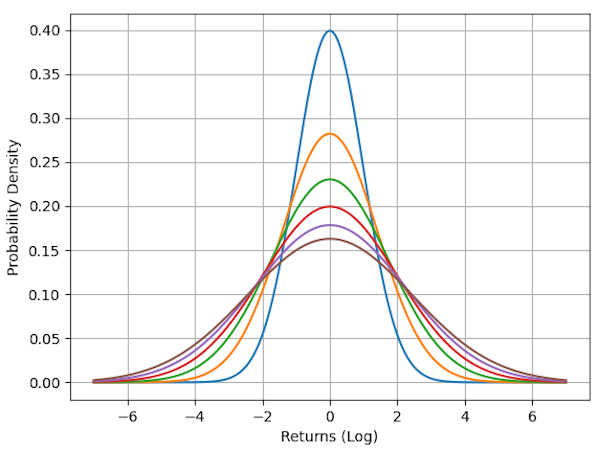
Each day into the future causes the resulting probability distribution to ‘spread out’ as uncertainty increases. The peak of the distribution gets lower each additional day, and the shoulders of the distribution get thicker.
By leveraging the techniques that have already been discussed like using the FFT, the computations can be performed quickly to model probabilities at future dates.
This method can also be used with Implied Probability distributions. Interested in learning more about Implied Probability? Check out my post on the topic!
Convolution Python Example
Using the Potion Analytics: THICC repository, we can quickly demo convolution using scipy distributions. The following code demo generates the return distributions plot in the previous section.
import matplotlib.pyplot as plt
from scipy.stats import norm
from potion.curve_gen.convolution.builder import ConvolutionConfigBuilder
from potion.curve_gen.convolution.convolution import (configure_convolution,
run_convolution, get_pdf_arrays)
# Specify our settings using the builder
builder = ConvolutionConfigBuilder()
# Normal distribution using mean 0 std dev 1, convolve 5 days into the future.
# Log only because we want to plot log returns and not prices. Min/Max X change the
# axis limits
builder.set_distribution_params(
[0, 1]).set_distribution(norm.pdf).set_num_times_to_convolve(5).set_log_only(True)
builder.set_min_x(-7.0).set_max_x(7.0)
# configure the convolution module
configure_convolution(builder.build_config())
# Run the convolution
run_convolution()
# Get the output arrays to plot
x_values, y_values = get_pdf_arrays()
# Plot the resulting PDFs
fig = plt.figure()
ax = fig.gca()
ax.grid(True)
ax.set_xlabel('Returns (Log)')
ax.set_ylabel('Probability Density')
for y in y_values:
ax.plot(x_values, y)
plt.show()
References
- Burrus, C. Sidney, and T. Parks. “Convolution algorithms.” Citeseer: New York, NY, USA (1985).
- Pierre, John W. “A novel method for calculating the convolution sum of two finite length sequences.” IEEE transactions on Education 39.1 (1996): 77-80.
- Cooley, James, Peter Lewis, and Peter Welch. “Application of the fast Fourier transform to computation of Fourier integrals, Fourier series, and convolution integrals.” IEEE Transactions on Audio and Electroacoustics 15.2 (1967): 79-84.
- Rényi, A. “On the central limit theorem for the sum of a random number of independent random variables.” Acta Math. Acad. Sci. Hung 11.1–2 (1960): 97-102.
- Johnson, M., Mosquera, G., & Munoz, J. (n.d.). Potion Bonding Curve Generation for Fat-Tailed Models Using the Kelly Criterion. Ntropika Labs.
- Greene, B. (2006, October 20). The universe on a string. The New York Times. Retrieved May 27, 2022, from https://www.nytimes.com/2006/10/20/opinion/20greenehed.html